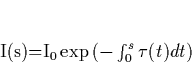

Next: Calculation Methods
Up: Fundamentals of Volume Tracing
Previous: Transfer Functions
Participating media may absorb, emit and/or scatter light.
The simplest participating medium only absorbs light. That means that light
passing through the medium is attenuated depending on the density of the
medium. Max [Max95] derives the following equation for a light
absorbing participating medium
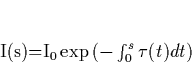 |
(1) |
which gives the light intensity 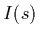 at distance
at distance 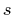 .
. 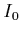 is the light
intensity at
is the light
intensity at 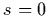 where the ray enters the volume.
where the ray enters the volume. 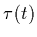 denotes the
extinction coefficient at position t in the medium, which gives the fraction
of light that is absorbed rather than let through.
A good example for light-emitting
media are hot particles in a flame. The amount of light which is emitted
along a ray can be described by
denotes the
extinction coefficient at position t in the medium, which gives the fraction
of light that is absorbed rather than let through.
A good example for light-emitting
media are hot particles in a flame. The amount of light which is emitted
along a ray can be described by
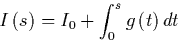 |
(2) |
where 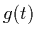 is called the source term.
is called the source term. 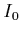 is the amount of light which
enters the medium. The integrated emission along the ray is simply added to
the light that entered the medium from the outside.
Real particles both absorb and emit light, so
the equations for absorption and emission have to be
combined. Max derives an equation which gives the intensity at the eye
is the amount of light which
enters the medium. The integrated emission along the ray is simply added to
the light that entered the medium from the outside.
Real particles both absorb and emit light, so
the equations for absorption and emission have to be
combined. Max derives an equation which gives the intensity at the eye
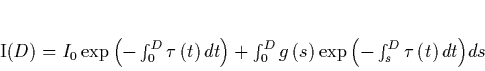 |
(3) |
Because participating media consist of small particles, light is not just
reflected or refracted by the medium, but scattered. That means that at
arbitrary points, light is scattered in different directions. The way light is
scattered is defined by so-called phase-functions. In order to understand
phase-functions, another term has to be defined. The particle albedo of a
participating medium gives the fraction of the
extinction which represents scattering rather than absorption. Clouds or snow,
for example, have a very high albedo and therefore appear very bright. Soot, in
contrast, has a very low albedo and therefore it appears very dark.
Phase functions describe the way light is scattered by a participating medium.
They return the fraction of light which is scattered from the lightsource into
the eye. Two different classes of phase functions can be distinguished -
isotropic and anisotropic phase functions. In an isotropic medium, light is
scattered uniformely in all directions, whereas in an anisotropic medium,
scattering depends on the angle between the incident and outgoing direction
of light. I.e. certain kinds of fog tend to scatter more light back to the
lightsource than in the forward direction. This phenomenon is called
backward-scattering.
In a medium with low albedo and low density it is unlikely that a ray of light
is scattered more than once before leaving the medium.
Therefore it is sufficient to consider only light that is scattered from the
light source directly into the eye.
In the simplest approach it is assumed that light reaches
the particles from a distant lightsource (or lightsources) and is not blocked
by objects or absorbed by the participating medium. Max gives a general
shading rule for this approach:
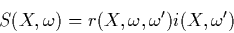 |
(4) |
where 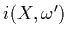 is the incoming light reaching
is the incoming light reaching 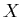 flowing in direction
flowing in direction
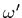 .
.
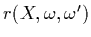 is the BRDF (bidirectional reflection
distribution function) which describes which fraction of the light coming in
from direction
is the BRDF (bidirectional reflection
distribution function) which describes which fraction of the light coming in
from direction 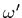 to point
to point 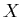 is reflected in the direction of
is reflected in the direction of
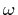 . A rule especially suited for volume rendering is
. A rule especially suited for volume rendering is
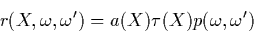 |
(5) |
where 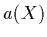 is the particle albedo,
is the particle albedo,
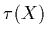 the extinction coefficient and
the extinction coefficient and 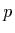 is the
phase function describing the directionality of the scattering.
The term
is the
phase function describing the directionality of the scattering.
The term 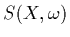 can simply be added to the source term
can simply be added to the source term 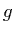
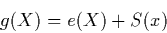 |
(6) |
where 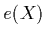 is the direct emission at position
is the direct emission at position 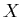 and
and 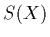 the
in-scattered light at position
the
in-scattered light at position 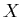 . If the source term is defined this way,
equation 3 can be used to handle direct
emission as well as scattering.
The above approach is quite simple, but does not account for shadows.
Clouds, for example, often appear darker on the side which is opposite to the sun,
because the clouds itself absorb light and shadow themselves from the sun.
In order to handle shaded scattering, equation
3 has to be refined. Max [Max95]
presents a solution, where a shadow-feeler is sent to the lightsource for each
point
. If the source term is defined this way,
equation 3 can be used to handle direct
emission as well as scattering.
The above approach is quite simple, but does not account for shadows.
Clouds, for example, often appear darker on the side which is opposite to the sun,
because the clouds itself absorb light and shadow themselves from the sun.
In order to handle shaded scattering, equation
3 has to be refined. Max [Max95]
presents a solution, where a shadow-feeler is sent to the lightsource for each
point 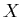 along the primary ray. Then, the amount of incoming light at each of
these points along the primary ray is diminished using the absorption value along
the shadow feeler.
To render even more accurate images, multiple scattering effects have to be
taken into account. This means, that light is scattered more than once
before it reaches the eye. In participating media with high albedo, like clouds,
the influence of multiple scattering cannot be ignored. Modelling multiple
scattering is a very demanding task - the problem is comparable to the radiosity
problem, but instead of surfaces which can receive light from all other
surfaces, volume elements receive light from all other volume elements.
In order to calculate multiple scattering effects,
different methods have been presented to calculate approximate
solutions [RT87],
[KV84], [Max95], [Sta95].
along the primary ray. Then, the amount of incoming light at each of
these points along the primary ray is diminished using the absorption value along
the shadow feeler.
To render even more accurate images, multiple scattering effects have to be
taken into account. This means, that light is scattered more than once
before it reaches the eye. In participating media with high albedo, like clouds,
the influence of multiple scattering cannot be ignored. Modelling multiple
scattering is a very demanding task - the problem is comparable to the radiosity
problem, but instead of surfaces which can receive light from all other
surfaces, volume elements receive light from all other volume elements.
In order to calculate multiple scattering effects,
different methods have been presented to calculate approximate
solutions [RT87],
[KV84], [Max95], [Sta95].


Next: Calculation Methods
Up: Fundamentals of Volume Tracing
Previous: Transfer Functions
2000-04-06