![[CESCG logo]](../../CESCG/images/cescg98.small.gif)
jet@inf.bme.hu
Department of Control Engineering and Information Technology
Technical University of Budapest
Budapest, Hungary
![[CESCG logo]](../../CESCG/images/cescg.small.gif)
![[CESCG logo]](../../CESCG/images/cescg98.small.gif)
|
Implementation of bidirectional ray tracing algorithm
jet@inf.bme.hu Department of Control Engineering and Information Technology Technical University of Budapest Budapest, Hungary |
![[CESCG logo]](../../CESCG/images/cescg.small.gif)
|
Keywords: Computer graphics, ray tracing, Monte Carlo methods, bidirectional ray tracing
Monte Carlo methods were also successfully applied in the field of radiosity methods. This topic is discussed in [SzFW98b] and [SzFTCs97]. An elegant solution was proposed in [SzFW98a] that computes the radiosity of patches with an infinite number of rays using global directions. However, radiosity-based methods do provide efficient solution only if the surfaces are mostly diffuse and the light sources are large. The decomposition of large surfaces into smaller patches represents an other problem, therefore a universal solution may become relatively complex compared to the methods discussed in this paper.
The goal of the ray tracing process is to determine the amount of light arriving to the observer through the pixels of the image. To do that, Monte Carlo ray tracing algorithms generate light transport paths in the object space that carry a given amount of light from a light source to the camera, and estimate the amount of incoming light with these sample light paths. Since our computational capacity is limited, we would like to compute the image by computing as little light paths as possible. To achieve this, we need an algorithm that generates paths that carry much light (and hence contribute to the final image significantly), and that does not generate paths that carry little amount of light.
After selecting a starting point, the algorithm chooses a random direction, and fires a ray into that direction, examining which surface is hit by the ray. When making further bounces, the further random directions are usually not chosen uniformly, but according to the Bidirectional Reflectance Distribution Function (BRDF) of the surface, i.e. the probability of choosing a direction is proportional to the BRDF. This method reduces the noise of the image since it is more likely to generate directions where the transmission is large. This idea is called importance sampling.
After a number of samples have been taken, the following equation is used to estimate of the integral:
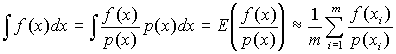
| (1) |
This method may produce an acceptable result, but a lot of scenes exist, where the noise level of the image generated will be far too big. To generate a path that contributes to the final image significantly, the path has to end in a light source. In case of point light sources, this would be impossible, so standard tracing techniques treat them specially, usually trying to fire a ray against all point light sources after each bounce.
If there are area light sources in the system, this tracing algorithm works fine only if the light sources are big, and the surfaces are nearly specular. In this case, the probability of randomly hitting a light source is large. But if the light sources are small and the surfaces are diffuse, the algorithm has almost no chance to hit the light source. This will introduce a lot of noise in the final image.
A very elegant and efficient method was presented in [VG95]. If we have n sampling techniques, we can construct an F function based on the wi weight distribution derived from pi probabilities so that the variance of F will be provably lower than the original one:
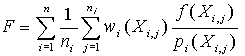
| (2) |
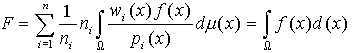
| (3) |
A more general light path generator algorithm was developed independently by Veach and Guibas [VG94, VG95] and Lafortune and Willems [LW93]. The algorithm generates light paths from both ends. One segment is built up starting from the camera while the other segment is starting from an arbitrary point on the surface of a light source. Finally, the two segments are connected with a deterministic step. The process is illustrated on Figure 2.4.
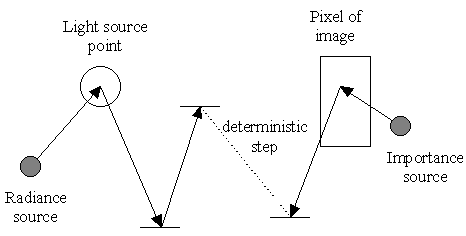
|
| Figure 2.4: The process bidirectional light path generation |
From the camera, the first step is to generate a point on the lens aperture. Currently, this is a single determined point, but we leave this step because further improvements may take use of this, e.g. motion blur can be introduced if the camera points are generated on a line segment. From the light source side, the first step is to generate a point on a light emitting surface. This approach allows only area light sources. (Point light sources could be introduced easily.) The number of camera and light source steps is pre-determined.
These methods applied for all possible camera path and light source path lengths give a number of ways to generate light paths. Theoretically, the number of bounces can be very big, put in practical cases, the paths that have a length of more than 4-8 (depending on the scene), do not contribute to the picture significantly, so they can be ignored. The transmissions of paths generated by different methods can be combined by the method described in the previous chapter ([VG95]).
Implementation problems of this method is further discussed in section 4.
The library has several demo applications:


|
| Figure 3.2a: Images generated with the single-step ray tracer. |

|
|
Figure 3.2b: Image generated with the standard Monte Carlo ray tracer. |
Existing Monte Carlo ray tracer implementations generally do not calculate the value of f and p separately, since only f/p is required in standard ray tracing methods (as seen in (2) ) that can be calculated at lower cost than determining f and p independently. However, the optimal combination of samples (section 2.3) from several sampling techniques requires the explicit value of pi to calculate the wi weights.
To determine the intensity value of a pixel in the image, a number of samples light paths are taken that go through the pixel. The integral is estimated with an improved version of the formula in (1). To calculate the estimated value, the evaluation of f(x) and p(x) is required for all generated light paths.
| Iout=Iin·BRDF(L,V)·cos(Theta) | (4) |
First, let us examine the case of standard Monte Carlo ray tracing, where rays are always traced backwards. In this case, p(x) can be calculated as a product of the values of the local probability functions: p0 is the value of probability density function of generating the first ray from the camera, while pi are the probability density functions of generating bounces respectively.

|
| Figure 4.2a: Calculating p(x) in the standard Monte Carlo case |
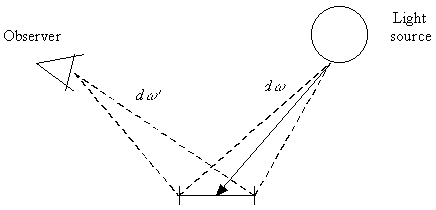
When tracing the path of light from the light sources, we need to calculate the same function. However, when tracing the path of light from the light sources, we do not generate the path according to these probabilities, so the probability density has to be transformed into our system. The transformation for the first step - when a random point is chosen on a light emitting surface - is shown on Figure 4.2b:
|
| Figure 4.2b: Transforming the probability of direct lighting component |
The transformed probabilities can be calculated with the following formulae:
|
| (5) |
|
| (6) |
For efficiency, light paths are not generated fully independently of each other: shorter paths are generated from longer paths by leaving steps out of them. This method does not introduce any visible artifacts to the image generated but reduces computational costs. The scenes shown below contain 12-17 geometric primitives while the computation time was between 60 and 90 minutes on a workstation for one image, with 200-300 samples per pixel in 640 x 480 resolution.
Figure 4.3a shows a Cornell-box like scene with an almost perfectly mirroring big metal ball and a smaller, purple but very shiny ball. Shadows are soft because of the large light source. Note that diffuse inter-reflection is also taken into account, the effects can be observed especially on the ceiling, where the colors of neighboring walls are reflected next to the light source.
Figure 4.3b shows a similar scene. The light source is much smaller but the intensity is bigger, so that the total flux emitted is the same as in the previous case. This shows that the method is equally suitable for small and large light sources. The small light ball to the right is an imperfect mirror. Note that not only the area light source, but the reflection of the walls are rendered in high quality.


|
| Figure 4.3a and 4.3b: Images generated with the bidirectional path tracer |

|
| Figure 4.3c: Light mirrored onto the floor |
Future work should should concentrate primarily on further improving the algorithm, examining current more advanced methods such as in [VG97]. Also, the implementation of both TrayLib and the bidirectional renderer can be improved in many fields.
| [LW93] | Lafortune, E. and Willems, Y.D.: Bi-directional Path-Tracing Compugraphics '93 |
| [Phong75] | Phong, Bui Thong: Illumination for Computer Generated Images Communications of the ACM journal, Volume 18, 1975 |
| [Shir91] | Peter Shirley and Wang : Direct Lighting Calculation by Monte Carlo Integration
Proceedings of the 2nd Eurographics rendering Workshop, Barcelona, 1991 |
| [Shri65] | Shrider, J. (editor): The Monte-Carlo Method Pergamon Press, Oxford, 1966 |
| [Szir95] | László Szirmay-Kalos:
Theory of three-dimensional computer graphics Akadémiai Kiadó, Budapest, 1995 |
| [SzFW98a] | László Szirmay-Kalos, Tibor Fóris, Werner
Purgathofer:
Quasi-Monte Carlo Global Light Tracing with Infinite Number of rays Winter School of Computer Graphics, 1998 |
| [SzFW98b] | László Szirmay-Kalos, Tibor Fóris, Werner
Purgathofer:
Non-diffuse, Random-walk Radiosity Algorithm with Linear Basis Functions Journal of Machine Graphics and Vision, 1998 May |
| [SzFTCs97] | László Szirmay-Kalos, Tibor Fóris,
László Neumann, Balázs Csébfalvi:
An Analysis of quasi-Monte Carlo Integration Applied to
the Transillumination Radiosity Methods Computer Graphics Forum, Vol 16, No 3, 1997 |
| [VG94] | Eric Veach and Leonidas J. Guibas:
Bidirectional Estimators for Light Transport Proceedings of Fifth Eurographics Workshop on Rendering, 1994 |
| [VG95] | Eric Veach and Leonidas J. Guibas:
Optimally Combining Sampling Techniques for Monte Carlo Rendering Proceedings of SIGGRAPH 95 |
| [VG97] | Eric Veach and Leonidas J. Guibas: Metropolis Light Transport Proceedings of SIGGRAPH 97 |
| [Ward95] | Greg Ward: The Materials and Geometry Format Lawrence Berkeley Laboratory, 1995 |